Page 108 - 南京医科大学学报自然科学版

第42卷第2期
·254 · 南 京 医 科 大 学 学 报 2022年2月

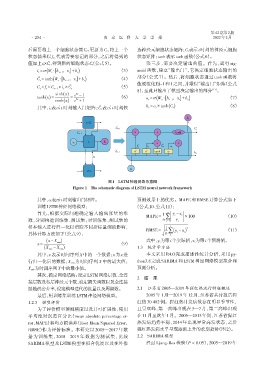
后需要将上一个细胞状态值Ct-1更新为Ct，将上一个 选神经元细胞状态矩阵；Ct表示t时刻的神经元细胞
状态值乘以ft，代表需要忘记的部分，之后将得到的 状态矩阵；tanh表示tanh函数（公式6）。
值加上it×Ct，得到新的细胞状态Ct （公式5）。 第三步，需要决定输出的值。首先，运行 sig⁃
i = σ(W ⋅[h ，x + b i ) （3） moid 函数，建立“输出门”，它决定细胞状态输出的
] t
t
i
t - 1
͂
C = tanh(W ⋅[h ，x + b c ) （4） 部分（公式 7）。然后，将细胞状态通过 tanh 函数将
] t
c
t
t - 1
值规范化到-1和1之间，并乘以“输出门”矩阵（公式
C = f × C t - 1 + i × C ͂ t （5） ［11］
t
t
t
sinh( ) x e - 1 8），至此只输出了模型决定输出的部分 。
2x
tanh( ) x = = 2x （6） o = σ(W ⋅[h ，x + b ) （7）
cosh( ) x e + 1 t o t - 1 ] t o
h = o × tanh( ) （8）
C
其中，it表示 t 时刻输入门矩阵； C t表示 t 时刻候 t t t
ht
t-1
Ct-1 Ct
× + tanh
Ct-1
t
xt ht
× ×
ft it Ct ot
σ σ tanh σ
ht-1
ht
n
xt
t+n
图1 LSTM神经网络示意图
Figure 1 The schematic diagram of LSTM neural network framework
其中，ot表示t时刻输出门矩阵。 预测效果上的优劣。MAPE 和RMSE 计算公式如下
训练LSTM神经网络模型： （公式10、公式11）：
首先，根据实际问题确定输入输出张量的维 1 n | y - x i |
i
MAPE = ∑ | | | |× 100 （10）
数，分别构造训练集、测试集；对训练集、测试集的 n i = 1| y i |
样本输入进行归一化以消除不同指标量纲的影响， 1 1 2
RMSE = ∑ (y - x i ) （11）
i
具体计算方法如下（公式9）： n n
(x - X ) 式中，yi为第i个实际值，xi为第i个预测值。
x = min （9）
(X - X ) 1.3 统计学方法
max min
其中，x表示时间序列X中的一个数据；x为x进 本文采用 R4.0 完成描述性统计分析，采用 py⁃
行归一化后的数据；Xmax为时间序列 X 中的最大值； thon3.8完成SARIMA 和LSTM 神经网络模型拟合和
Xmin为时间序列X中的最小值。 预测分析。
其次，确定网络结构：设定LSTM网络层数、全连
2 结 果
接层数及各层神经元个数，设定损失函数以及全连接
层随机舍弃率，设定模型迭代的批量以及周期数。 2.1 江苏省2005—2019年猩红热流行特征概述
最后，用训练集训练LSTM神经网络模型。 2005年1月—2019年12月，江苏省共计报告猩
1.2.3 模型评价 红热30 482例。猩红热月发病数存在明显季节性，
为了评价模型预测精度以及其可扩展性，使用 且呈双峰，第一高峰出现在 3—7 月，第二高峰出现

平均绝对误差百分比（mean absolute percentage er⁃ 在11月至次年1月。2005—2013年间，江苏省猩红
ror，MAPE）和均方根误差（Root Mean Squared Error， 热发病趋势平稳，2014 年出现异常高发状态，之后
RMSE）作为评价标准。本研究以 2005—2017 年数 猩红热发病水平呈现逐渐上升的长期趋势（图2）。
据为训练集，2018—2019 年数据为测试集，比较 2.2 SARIMA模型
SARIMA 模型及 LSTM 模型在拟合优度以及在外推 经过 Ljung⁃Box 检验（P < 0.05），2005—2019 年